Abstract: Generative adversarial network (GAN) has shown siginificant imporvments of learning latent representation of high-dimensional continuous data such as images and videos. Many amazing applications such as video synthesis and image translation are based on the capability of GAN. Unfortunately, applying GAN to discrete input remain a challenging problem. One of reasons is the discrete nature of data prevent the discriminator from providing useful gradient information for learning. In this post, I will foucus on some recent techniques to address this difficulty in the text generation and the evaluation
A rapid development of GAN (GAN zoo) has been applied to many amazing applications in the continuous data such image. They can be used to do image translation or even creative art, A recent workshop on ECCV 2018 just dedica

However, the development of GAN and its application in discrete data such as text is far from explored. In general, it is the discrete nature of text that makes apply GAN to such data difficult. According to Goodfellow, the generator learns how to slightly change the synethetic data through the gradient information from the discriminator. Such slight change is only meaningful for continuous data. For example, it is resaonable to change a pixel value from 1 to 1 + 0.001 while it is not for changing “penguin” to “penguin” + 0.001.
Recently, several approaches for text generation have been proposed to address this issue and some of them have many interesting results. In this article, I will give an overview of these methods, evaluation and their applications.
Table of Contents
Model for text generation
Improved training of GAN
Perhaps the most basic task to study the capability of generating meaningful text is to generate simple characters with certain pattern. Kusner et al. [1] proposes to relax the output multimodal discrete distribution for each time step $t$ in RNN decoder by using Gumbel-softmax, which is a continuous approximation.
\begin{align} \label{eq:1} \boldsymbol{y}_{t} = \textrm{softmax}(\frac{ \boldsymbol{h}_t + \boldsymbol{g}_t}{\tau}) (1), \end{align} where $\boldsymbol{h}_t$ is the hidden statet of RNN decoder in $t$ step and $\boldsymbol{g}_t$ is sample from the Gumbel distribution. $\tau$ is a parameter used to control how the close the continuous approximate distribution to the discrete one. When $\tau \rightarrow 0$, Eq (1) is more like to discrete distribution. When $\tau \rightarrow \infty$, it is more like a uniform distribution. We call this Gumbel-softmax trick. Here are some great tutorial by Erig Jang and Gonzalo Mena if you want to learn more about it.
The result of using Gumbel-softmax seems help GAN in discrete space. As demonstrated Fig 1 clipped from the original paper, the left plot shows the samples generated by MLE and the right one is generated by proposed method which generate similar pattern shown in training data, especially for 4th, 10th and 17th row.


Several recently proposed approaches have shown further improvement of training GAN in discrete space . Hjelm et al. propose boundary seeking GAN (BEGAN)~\cite{} that uses discrimator optimized for estimating f-divergence. They use policy gradient and importance weight derived from the discriminator to guide the generator. Concurrently, Mroueh et al. propose Sobolev GAN~\cite{} that train GAN with new objective with Sobolev norm. Their results are still cannot generate readable sentences1.
But what could we get if we try not to be too harsh to our model and allow it to be pre-trained first on some corpus?
The textGAN proposed by Zhang et al. answers this question. They initialize the weights of LSTM generator from a pre-trained CNN-LSTM autoencoder (i.e. Using the weights of LSTM part to initialize the generator). Inspired by feature matching techniques used to improve GAN in the early day, they train the generator to synthesized data that match empirical distribution of the real data in the feature space by minimizing maximum mean discrepancy (MMD), which can be understood to minimize the moments of two distributions. If the Gaussian kernel is used (which is the case in the paper), it is shown that minimizing MMD will match moments of all orders of two distributions~\cite{}. Figure below shows the result of textGAN, we can see the generator can output some meaningful sentences. In addition, the trajectory of latent space is more resonable and smooth from one sentence to the othter compared to vanila autoencoder, which suggests textGAN learned better representation of text.

Standard GAN framework is designed for continuous data. Applying it to discrete data directly need to reformulate the learning objective or use pretraining to facilitate the learning. Is there any generative model that naturally fit the discrete input data? I will discuss it in the next section.
Variational Autoencoder
Unlike GAN, Variational Autoencoder (VAE) can work with both continous and discrete input data directly. For peolpe who are not familiar with VAE, I recommend the tutorial (here and here) written by Jaan Altossar and Blei et al.(if you want to go deeper). Here I just give a brief introduction. Given data $\boldsymbol{x}$, latent variable $\boldsymbol{z}$, encoder parameters $\boldsymbol{\theta}$ and decoder parameters $\boldsymbol{\phi}$, the goal of VAE is to approximate the posterior $p(\boldsymbol{z}|\boldsymbol{x})$ by a familiy of distribution $q_\lambda(\boldsymbol{z}|\boldsymbol{x})$, where $\lambda$ indicates the familiy of distribution. Take Gaussian for example, $\boldsymbol{\lambda} = (\boldsymbol{\mu}, \boldsymbol{\sigma})$. This is achievied by maximizing the evidence lower bound (ELBO). For a single data point $x$, the ELBO is \begin{align} \textrm{ELOB}_i = \mathbb{E}_{q_{\theta}(z|x_i)}(\textrm{log}p_{\phi}(x_i|z)) - \textrm{KL}(q_{\theta}(z|x_i)||p(z)) \end{align} The first term can be viewed as how well the model can reconstruct data given the learned representation. The second term can be viewed as a regularization which we hope the learned posterior can be close to prior. Maximizing ELBO will encourage the model learn useful latent representation that explain the data well. Note that we use $q_{\theta}$ to replace the $q_{\lambda}$ since we use encoder to inference $\lambda$
Actually, the recent generative model for text is based on VAE proposed by Bowman et al. They propose a RNN-based variational autoencoder which capture the global feautre of sentces (e.g., topic, style) in continous variables. The RNN-encoder inference the $\mu$ and $\sigma$ of Gaussian and a sample $z$ is draw from the posterior for decoder to generate the sentences. The architecutre is shown below and many subsequent works follow similar architecture with some modifications.
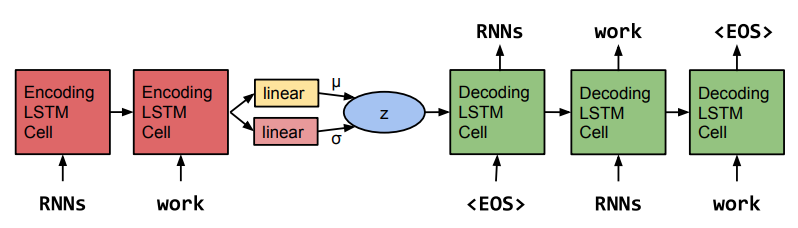
The core issue of using VAE in text generation is latent variable collapse, which means the KL term in the ELBO become zero during the optimization. This might seem to be confused at first since zero KL term seems to be beneficial to ELBO as we hope to maximize it. However, if we examine the KL term carefully, zero KL term means that the posterior $q_{\theta}(z|x_i)$ is equal to prior $p(z)$ thus posterior is independent from the input data! Latent variable collapse thus preclude us from learning useful latent representation from the input data which is a goal we aim to achieve. This is a common case in language modelling as discussed in~\cite{}. Once this happened, the RNN decoder will completely ignore the latent representation and naively use decoder’s capability to achieve the optimal. The difficulty here is how do we maximize the ELBO and prevent the KL term from going to zero at the same.
Bowman et al. propose KL-annealing and word dropout to alleviate this issue, which increase the weight of KL term during training and randomly replace word token by <UNK> to force decoder to rely on global representation $z$ instead of learned language model. However, these techniques cannot solve this issue and VAE trained in this way is slightly worse than language model (RNNLM) in NLL despite it can geenrate more plausible sentences and more smooth transition than autoencoder when moving in the latent space. Therefore many this line of research focus on finding better techniques to address latent variable collapse and I will dicuss them later.
Yang et al. hypothesize and validate the contexual capacity of decoder is related to latent variable collapse. They replace original RNN decoder with dilated convolutional neural network as the figure below, which facilitates the control of contextual capacity by changing dilation.
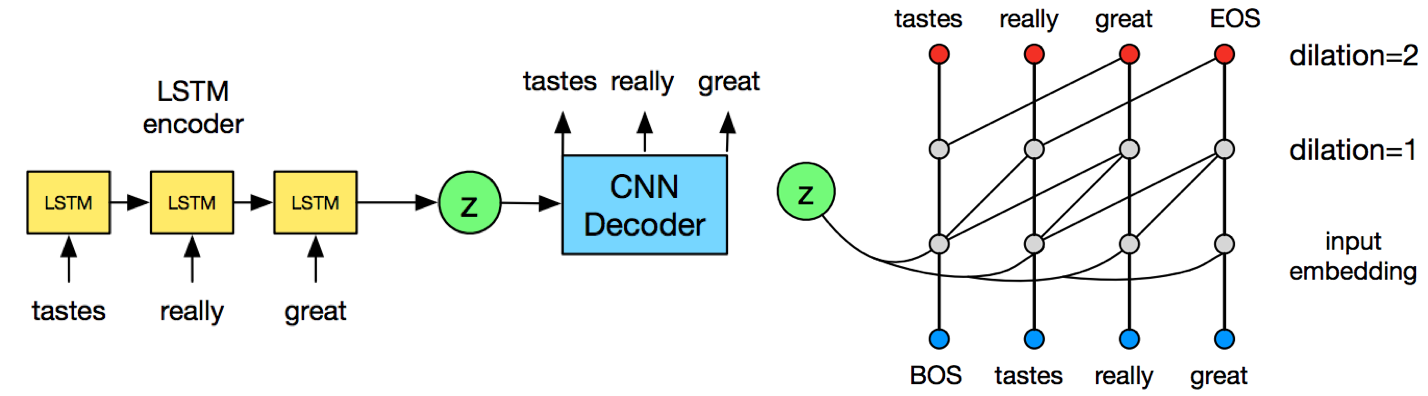
The dilated CNN used in the decoder is 1D dilated CNN, which is a way to enlarge the reception field without sacrifying computation cost. By controlling the dilation size in CNN. The author study 4 configurations of decoder with following depth and dilation: [1, 2, 4], [1, 2, 4, 8, 16], [1, 2, 4, 8, 16, 1, 2, 4, 8, 16] and [1, 2, 4, 8, 16, 1, 2, 4, 8, 16, 1, 2, 4, 8, 16], which are denoted as SCNN, MCNN, LCNN and VLCNN. They also compare with vanilla VAE proposed by Bownman et al. In each configuration, they further divide 3 training methods for comparison, which are: language model (LM), VAE (architectures proposed in this paper) and VAE + init that initalize the encoder’s weight by language model. The results are shown in Fig. 6
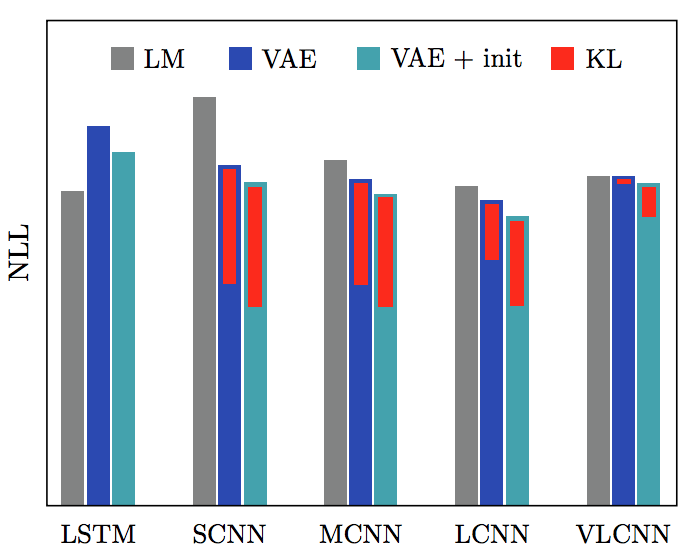
The vanilla VAE has worse NLL as KL term goes to zero which agrees with the the negative results found by Bowman et al. For the rest baselines based on CNN with different configurations (i.e. dilation, depth), we can see better improvement for small model (SCNN) over pure LM and the improvement gradually diminish as model size become large (VLCNN). This finding suggests that using dilated CNN as decoder could alleviate latent variable collapse if we carefully choose the decoder contextual capacity. Using pretrained language model also helps for the learning.
The latent space learned by proposed VAE by setting dimension of $z=2$ on Yahoo and Yelp review dataset is visualized in Fig.7. It’s interesting to see different topics are mapped to different regions and the sentiments (i.e. rating from 1-5) of review are horinzontally spread. The author extend the proposed method to conditional text generation. Some examples are presented in Fig. 8.


Concurrently, Semeniuta et al. propose a convolutional-deconvolutional VAE with recurrent models on top of the output of deconlolutional layers (Hybrid VAE) in Fig. 9 for text generation.
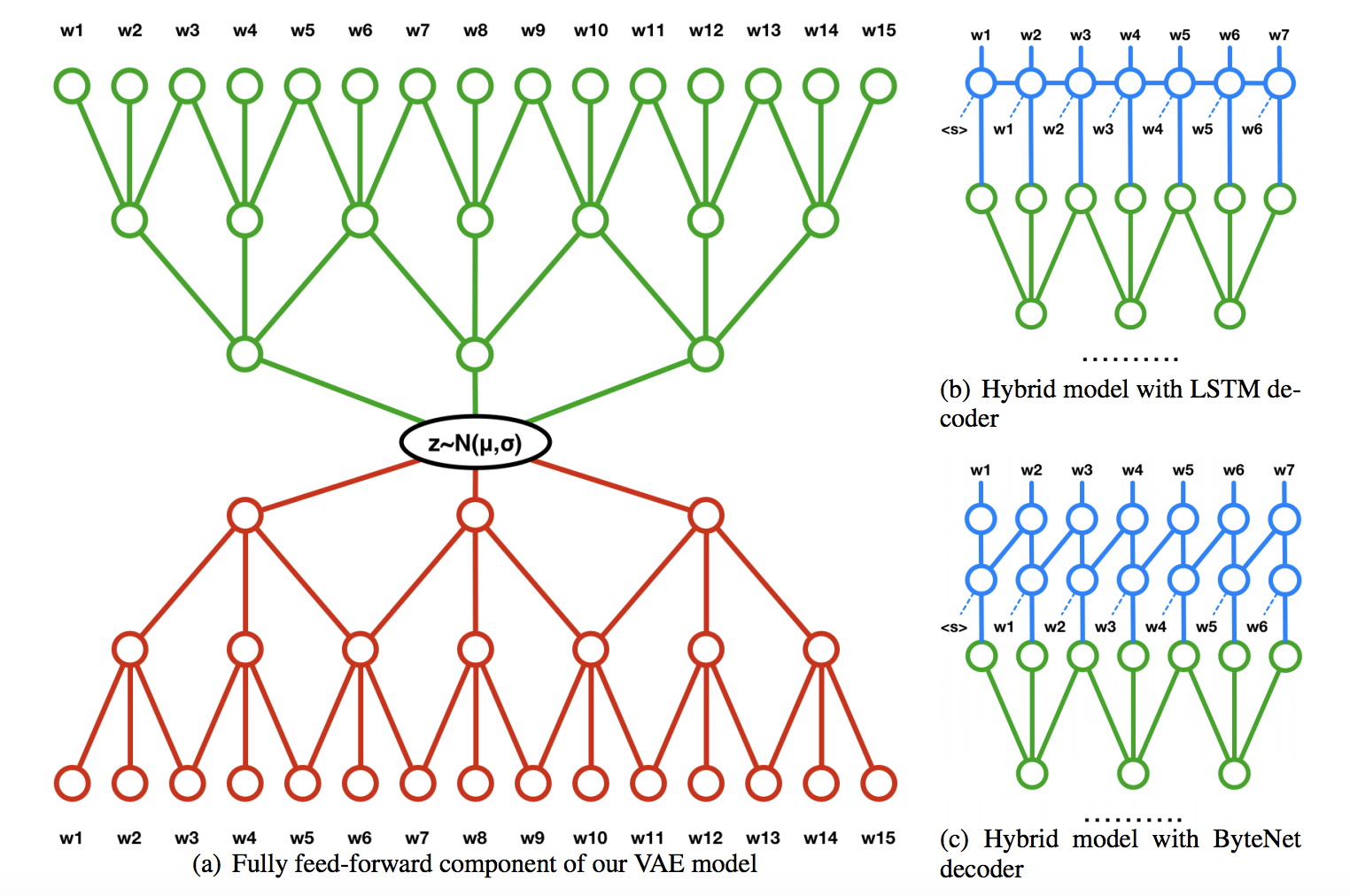
They further introduce an auxiliary loss $J_{aux} = -\alpha\mathbb{E}_{q(\boldsymbol{z}|\boldsymbol{x})}\textrm{log}p_{\phi}(\boldsymbol{x}|\boldsymbol{z})$ into the optimization of ELBO to force the decoding process rely on the latent representation $\boldsymbol{z}$. $\alpha$ is a parameter to control the penalty of auxiliary loss.
In their experiments, the compare the decoding performane of proposed method with vanilla VAE under historyless and history setting. In other words, they test the decoding performance of models by using word dropout rate $p$ from 1.0 to certain ratio during training (i.e. Randomly replacing the ground truth with <UNK> token during training). They also study the benefit of auxilary loss for decoding performance as the expressive power of decoder become stronger (i.e. deeper layer). The results are shown in Fig 10.
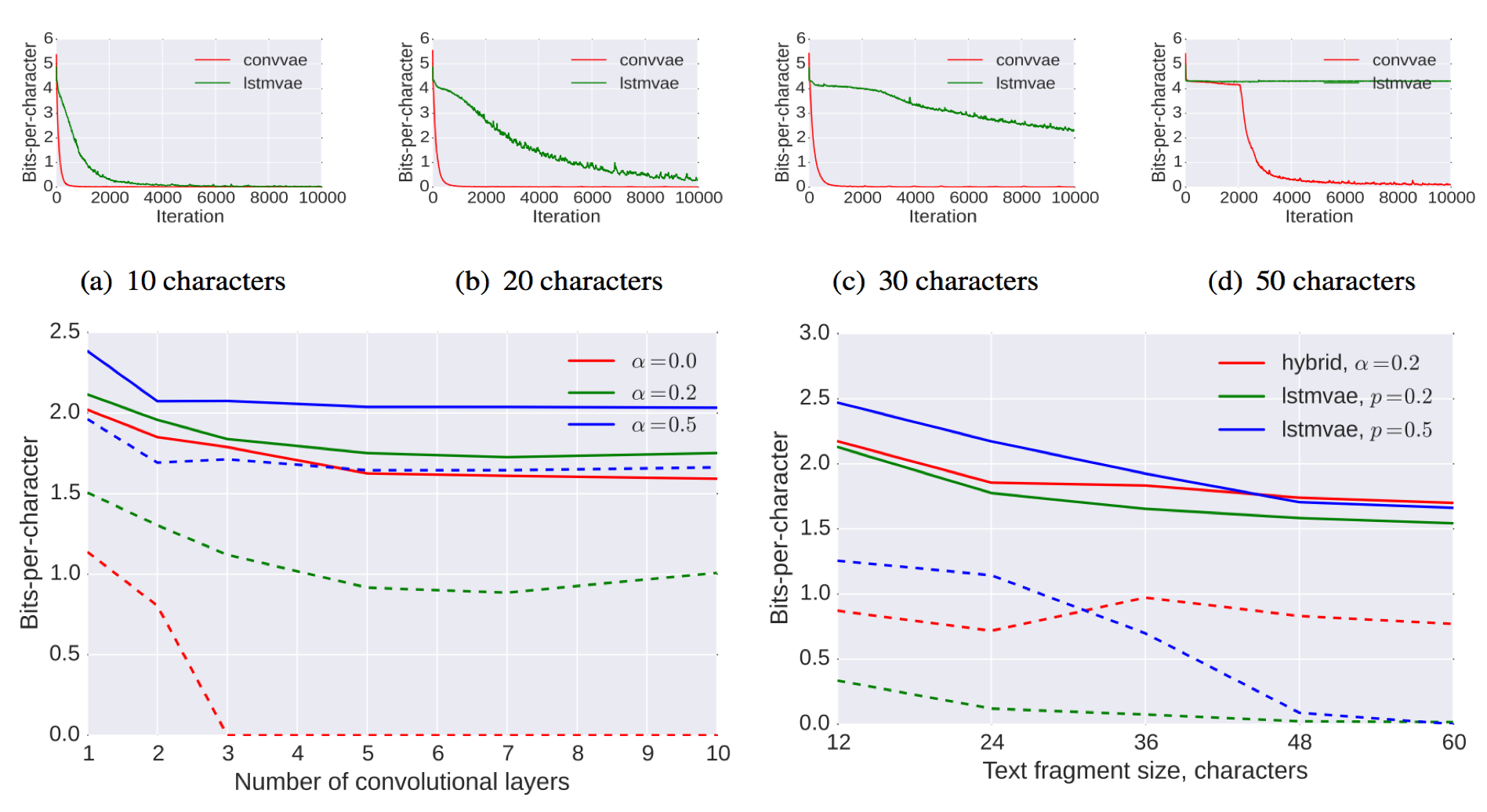
We can see that the hybrid VAE converge far faster and better than LSTM VAE no matter the length of text (Up). The proposed auxilary loss can prevent the KL term from 0 which allow us to train deeper (more powerful) decoder without latent variable collpase (Bottom left). The last figure (Bottom right) demonstrates that the Hybrid VAE perform similar to LSTM-VAE in terms of bits-per-character. However, the KL term of Hybrid VAE is not zero while it is alomost zero for LSTM-VAE, which suggest LSTM-VAE more serious latent variable collapse issue than Hybrid VAE.
Finally, developing new methods to address the latent variable collapse is still an very active research area. In ICML 2018, Kim et al. propose semi-amortized inference that initializing variatoinal parameter by amortized inference then applying stochastic variational inference to refine them. Dieng et al. introduce skip connections between latent variables $\boldsymbol{z}$ and decoder to enforce the relationship between latent variables and reconstrunction loss. Both methods are justified better than previous method by experiments. One most recent and exicting work proposed by Xu et al. in EMNLP 2018 conduct detail experiement and discussion about applying hyperspherical VAE on text generation~cite{}. By replacing gaussian prior with von mises fisher distribution, it is shown that the KL term can be totally control by hyper parameter $\kappa$ and therefore totally avert the latent variable collapse and this $\kappa$ is not sensitive to tasks.
Adversarial Regularized Autoencoder
Autoendoer is a naive model for learning latent representation of data. As mentioned in~\cite, applying it to learn text will result in non-smooth transition in the latent space, which lead to development of VAE and related techniques to improve it. Recently, a recent work deviates from this line of research. Zhao et al. propose Adversarially Regularized Autoencoders (ARAE) which extends the adversarially autoencoder to discrete data by adding learned prior to achieve some interesting applications. One of them is a reminiscent of conducting vector arithmetic of attribute in latent space in the early development of GAN, which means: smiling woman - normal woman + normal man = smiling man.

Similarily, the authors change “attribute” of sentence (i.e. Subject, verb and modifier) by similar vector arithmetic. They first generate 1M sentences by ARAE and parse the sentences to get subject, verb and modifiers. To substitute the verb, say sleeping, with running in a sentence. They first substract the mean latent vector of all sentences which contain sleeping from original sentence then add the mean latent vector of all sentences which contain running. The results are in Fig 12.
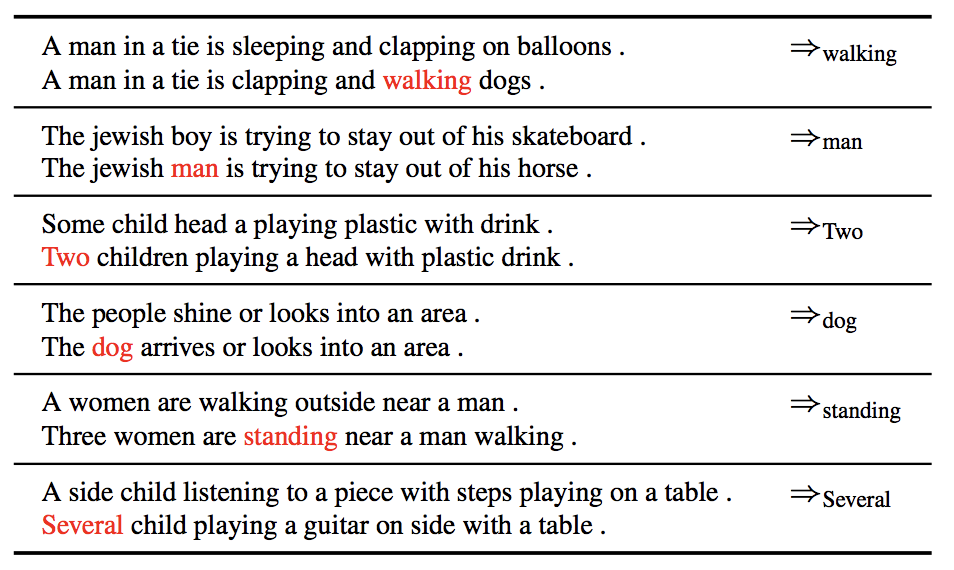
Although the text generated after the vector arithmetic is somewhat not plausible, it is the same for such task in the image data as shown in Fig 11. In my opinion, I found this progress made by ARAE very interesting because it remind me of the early development of GAN for image and I expect to see futrue improvement can generate more fluent sentences.
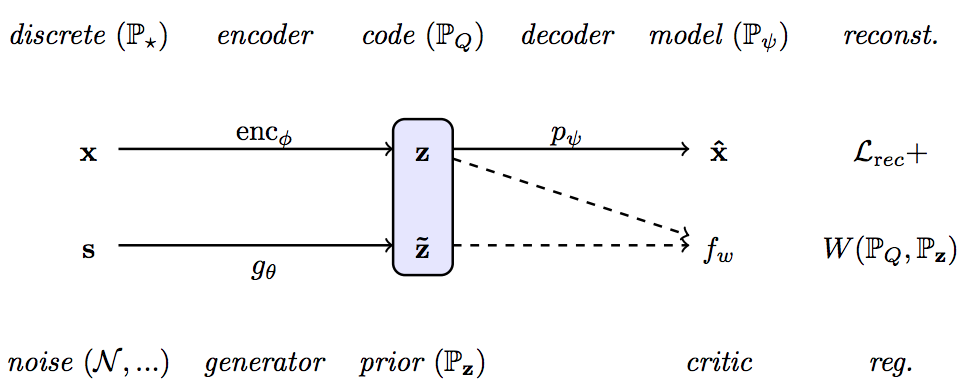
The high level idea of ARAE is illustrated in Fig. 13. Given a encoder, a generator, a decoder, and a critic parameterized by $\phi$, $\theta$, $\psi$, $w$, the goal is to learn a model which can map real discrete data $x \sim \mathbb{P}_{\star}$ to a latent code $z$ that is indistinguishable from a prior $\tilde{z}$ generated from a noise $s$. It is achieved by minimize the reconstruction loss of autoencoder regularized with a prior $P_{z}$, which is
\begin{align}
\textrm{min}_{\phi, \psi}~\mathcal{L}_{rec} + \lambda W(\mathbb{P}_{Q}, \mathbb{P}_{z})~,
\end{align}
$W$ is Wasserstein distance between two distributions and is computed by critic function $f_w$ which is adversarially trained by encoder $\phi$ and generator $\theta$. \lambda is just a hyperparameter to control the strength of regularization. For simiplicty, $w$ and $\theta$ are not shown above but are trained during optimization of critic and encoder. Please check the paper for more theoretical results and implementation details.
Reinforcement Learning
In the previous sections, the approaches applied to text generation is within the scope of traditional generative model like GAN, VAE and autoencoder. From this section, I will discuss another line of reaesech that cast text generation as a reinforcement learning problem. Under this scenario, the generator (decoder) is treated as an agent and the next token to output is viewed as next action to take given the current state. The goal of the generator is to maximize the total reward. Many works~\cite{} are proposed based on this framework and use task specific score (e.g, BLEU, ROUGE) as reward to train the agent.
Recently, Yu et al. extend previous works and propose SeqGAN, which is a more GAN-like method compared to the previous. In SeqGAN, the goal of generator $G_\theta$ is to fool the discriminator $D_\phi$ by generating fakse sequences $\tilde{s} \sim p_{G}$ which are indistinguishable from the real ones $s \sim p_{data} $ to maximize total reward $R(\tilde{s})$. The discrimiator tries to distinguish the real and generated sequences. Therefore, the reward signal to guide the agent is a score to measure how close the generated sequences to the real ones. A naive choose of this score is to view the discriminator as binary classifer (i.e. real and fake) and use the softmax value of the real class. Formally,
\begin{align} G_{\theta}: \textrm{ argmax}_{\theta}R(\tilde{s}) = \textrm{argmax}_{\theta}\sum_{t=0}^{n-1}r_{t}\textrm{log}p_{G_{\theta}}(w_{t} | w_{0:t-1}) \end{align} \begin{align} D_{\phi}: \textrm{ argmin}_{\phi}-\mathbb{E}_{s \sim p_{data}}\textrm{log}(D_{\phi}) - \mathbb{E}_{\tilde{s} \sim p_{G}}(1 - \textrm{log}D_{\phi}) \end{align}
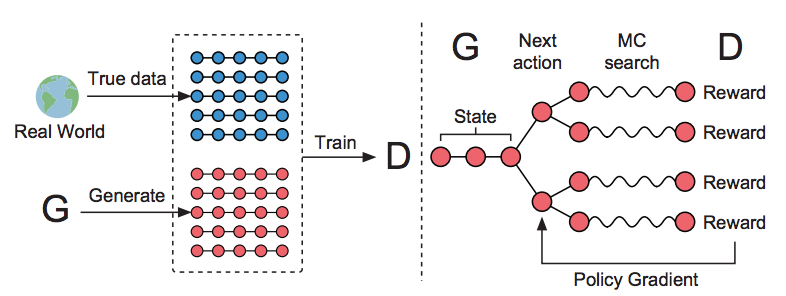
A question comes up is how do we get the intermediate reward before the sentences is completed ? It is as if it is hard to know whether the next move we take will help us win or lose in Go. To estimate this reward, SeqGAN applies Monte-Carlo search to roll-out current policy to estimate the reward as shown in Fig 14. The agent use the current learned policy network to roll-out several times till the end of sentences to get the estimated reward. One advantage of this design is that it is difficult to define a good reward for some tasks like poem and music generation. By using the output from generator as reward signal, we can bypass this issue.
One difference SeqGAN differs from GAN is it relies on pretraining on corpus to initialize the agent. Similar to GAN, the performance of generator is highly susceptile to the training strategies of generator and discriminator. We might get worse peroformance than MLE if we fail to orchestrate the training of generator and discriminator well. Fig. 15 shows different training strategies (i.e. how frequently the generator and discriminator update their parameters) on the synthetic dataset.
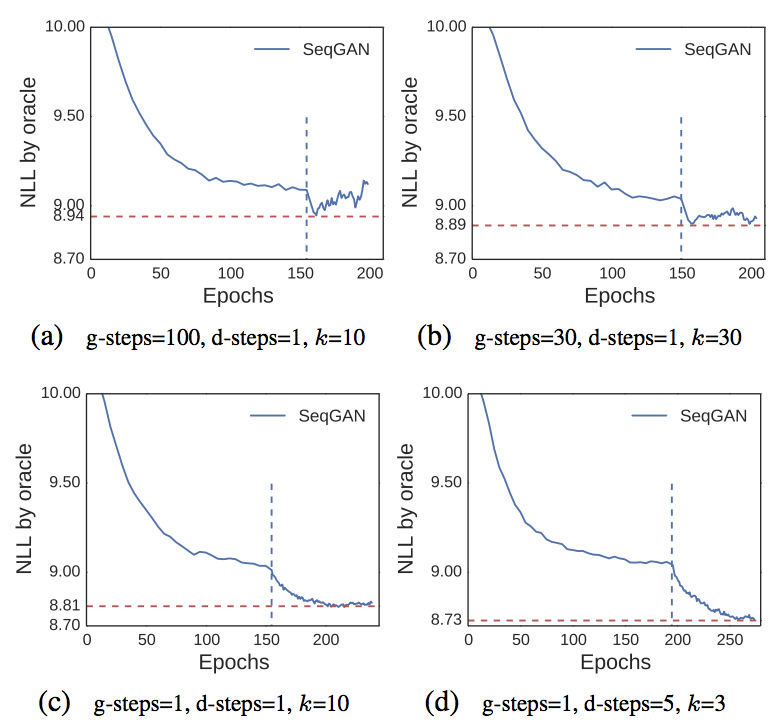
SeqGAN also suffers similar issuses reported in VAE and GAN. Gradient information from discriminator might be insufficient to guide the generator in some situations. For example, when the discriminator is too strong, most generated samples are classified as fake thus generator cannot learn to generate real sample by using gradients from discriminator (Most of them would close to zero). Mode-collapse also happens when generator greedily generate the tokens which maximize the reward thus lack of the diversity. generator greediliy ouptut the word that maximize the reward. I will first go through methods proposed to alleviate the first issue then the second one.
Che et al. propose MaliGAN~\cite{}, which extends~\cite{} to design a renoralized MLE objective. They prove that this new objective can provide better training signal even if the discriminator is less optimal (i.e. $D$ ranges from 0.5 to $p_{data}/(p_{data} + p_{G})$). In short, MaliGAN use $r = D(\tilde{s}) / 1 - D(\tilde{s})$ to calculate reward instead of binary score. The proposed method has better performance than SeqGAN on poem generation by 3 BLEU. The author did not report other comparisons to SeqGAN.
Lin et al. propose another modifcation of reward function by training a adversarial ranker instead of a discriminator. Similar to the framework of SeqGAN, the goal of generator is to produce sentences ranked higer than real ones to get higer ranking score while the ranker try to learn to rank the generaten sentences lower than the real.
Given input sentences $s_i$ , reference sentence $s_u$ from a reference set $U$ which contains all real sentences, the ranking score $R_{\phi}(s|U, C)$ is calculated by:
\begin{align} \alpha(s_i|s_u) = \frac{s_i \cdot s_u}{||s_{i}||s_{u}||}\textrm{, }P(s|u, C) = \frac{\textrm{exp}(\gamma\alpha(s|u))}{\sum_{s^{\prime} \in C^{\prime}} \textrm{exp}(\gamma\alpha(s^{\prime}|u))} \end{align} \begin{align} R_{\phi}(s_i|U, C) = \mathbb{E}_{u \in U}P(s_i|u,C) \end{align}
The final score of input sentence $s_i$ is the expectation over the whole reference set, which is contruced by randomly sampling real setences during learning. This simple modification of loss improve SeqGAN in various task as shown in Fig 16. RankGAN has better performance on synthetic data, Chinese poem generation, coco-caption generation in BLEU and human study. They also have better BLEU score on generate Shakespear play.
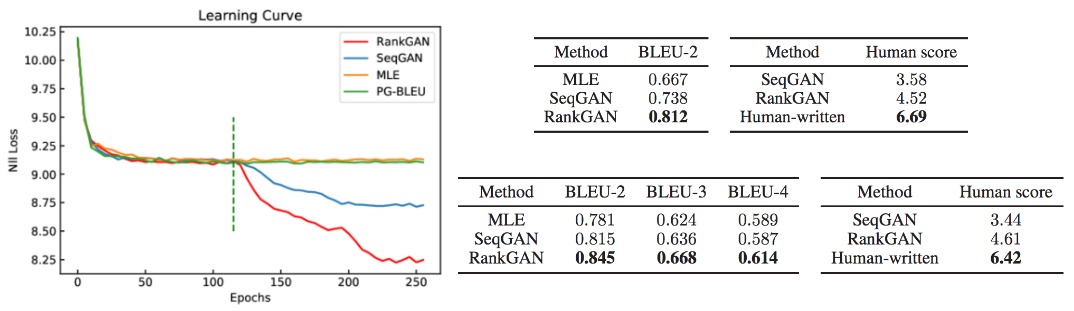
Despite the improvements bring by these methods, there are still two challenges: The first is using scalar as score might not be informative enought to guide the generator as it cannot well represent the intermediate structure of text during generation process. The second is estimating the intermediate reward tends to be noisy and sparse especially in long text generation where generator get reward only when entire sentences are finished.
Guo et al. propose LeakGAN that combines feature matching in~\cite{} and hierarchical reinforcemne learning to mitigate these challenges. A bird eye’s view of LeakGAN is illustrated in Fig. 17:
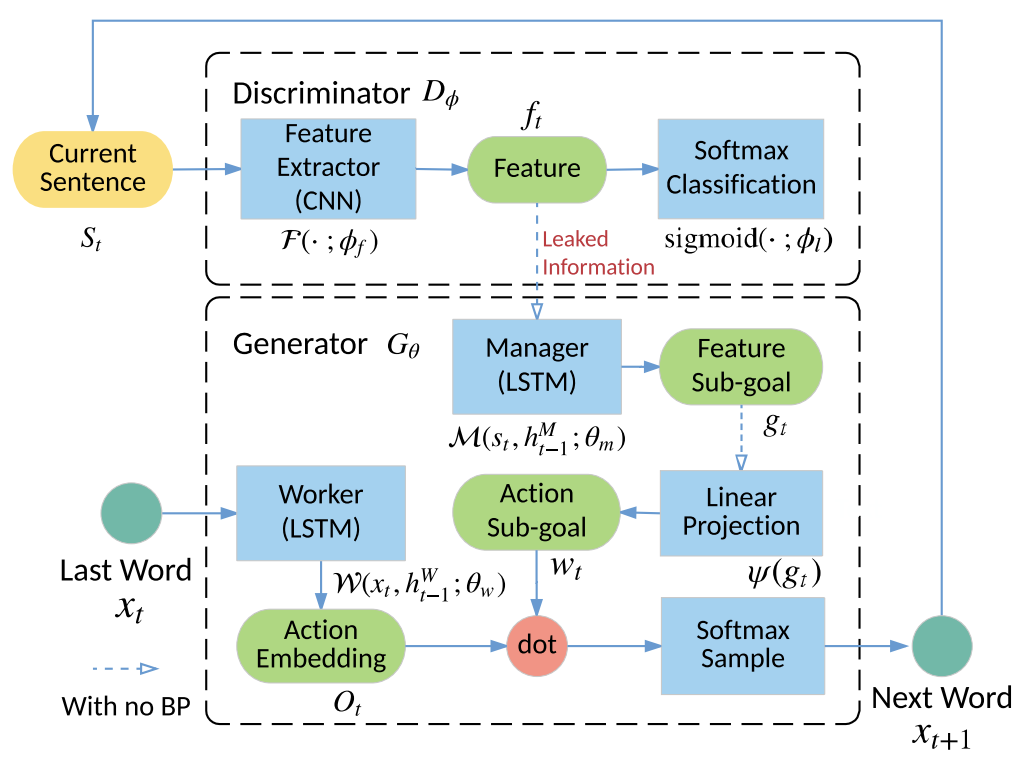
Given generator $G_{\theta}$ (bottom dotted-line) and $D_{\phi}$ (upper dotted-line), the generator is broken into Manager ($\mathcal{M}$) and Worker module ($\mathcal{W}$). To generate next word $x_{t+1}$, the current sentece $S_{t}$ is first fed into feature extratctor $\mathcal{F} $inside $D_{\phi}$. The extracted feature then leak to manager in the generator to compute a goal vector projected to action space $w_{t}$ by a linear projection $\psi$. The worker comptute the probability distribution of next action to take $O_{t}$ given the previos word $x_{t}$ then adjust its distribution by element-wise dot with $w_{t}$ to get final distribution.
In plain language, the worker is like a miscreant who forges the money and the disciminator is like police to detect it. The manager act as spy to leak the information police used to detect fake money during period $t$ for miscreant whenever the miscreant attempt to forge money in next period.
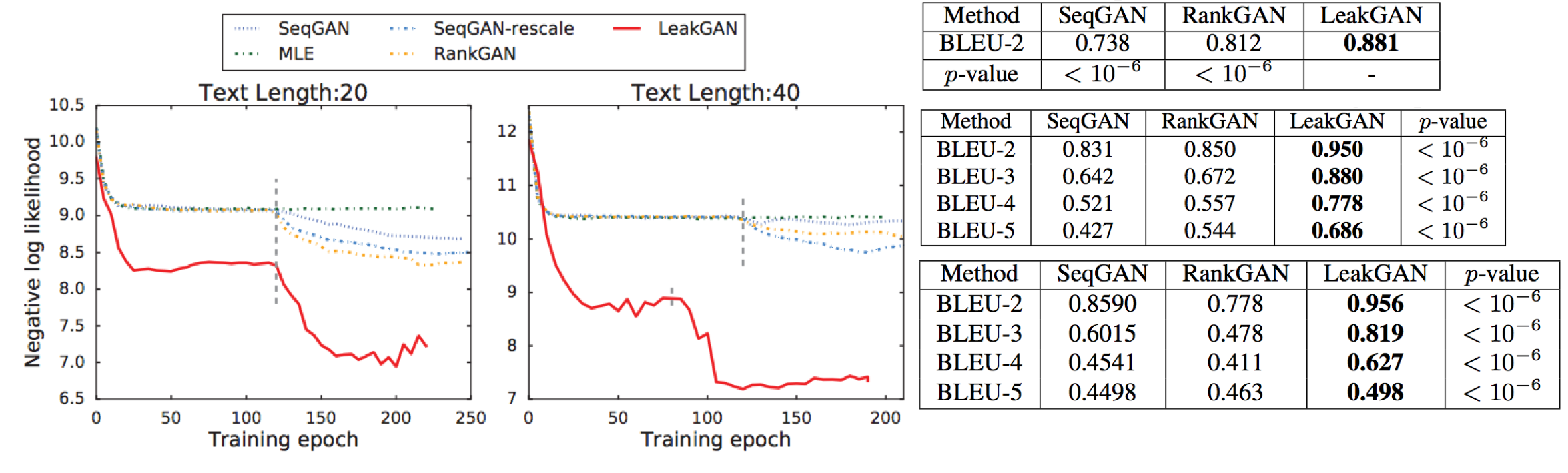
We can see big performance gain on both synthetic dataset and real dataset with average length from short to long in Fig. 18.
One interesting result in LeakGAN is that we can explore whether generator exploit the leaked information from discriminator to generate the data. This can be visualized by projecting the extract feature of real data and the text generated during period $t = 0$ to $t = T$, where T denote the timestep when sentence is completed. We call this process feature trace as termed by authors. Fig. 19 shows the result. We can see the features extraced from generator become more and more close to the real data as the generation process complete while other baselines fail to match it.
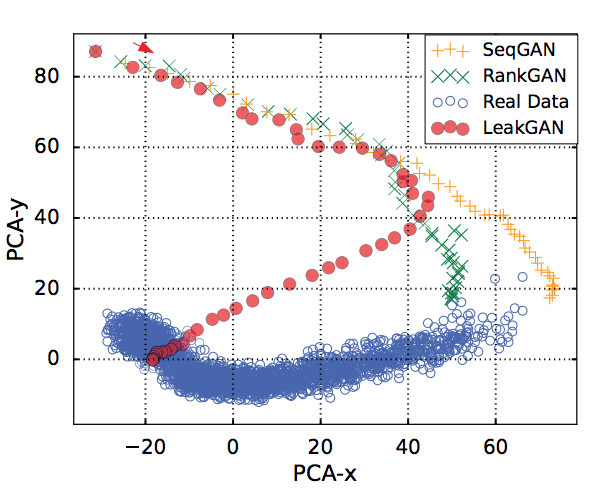
All methods above attempt to leverage more information from discriminator effectively to generate better quaility text, however, the mode collapse issue has not yet been explored in these works. In a recent survey~\cite{}, Zhu et al. observe that all methods above suffer from serious mode-collapse by measuring self-BLEU score, which is calculated by picking one generated sample then compute average BLEU score over generated samples collection.
Fig. 20 shows the BLEU score of above methods and self-BLEU on EMNLP2017 WMT. We can see that all methods discussed above suffer from serious mode collpase except MaskGAN. However, MaskGAN achieve lowest BLEU score on same dataset. This raise an important question:
HOW DO WE EVALUATE OUR TEXT GENERATION MODEL?
This will be discussed further in the evaluation part. Before diving to that, I would like to introduce MaskGAN to close this section.

The concept of MaskGAN[1]is learning to generate text by filling the blank. Instead of generating text unconditionally like previous methods, MaskGAN use a Seq2Seq to architecture for encoding masked text and generate text to fill in the blank. The disciminator also uses the same architecture. Fig. 21 shows the high-level picuture of MaskGAN.

The goal of generator is to predict the token given the masked sentence and what it has filled in. Different from the prior works, the discriminator here takes the generatd text and masked sentence as input to output a scalar to determine fake or real in every time step. An advantage of this design is the generator only get more punished on the error token which causes the entire sentence from real to fake. The tokens generated before this token will not be punished. The reason of why incldue masked input in discriminator is to help discriminator to deal with the following case as illustrated in the paper: If the generator output the director director guided the series, it is ambiguous of which director is fake because the director expertly guided the series and the associate director guided the series are valid sentence. The masked input can tell the discriminator which contetx of the real sentence.
Formally, given a input sequence $\boldsymbol{x} = (x_1, \cdots, x_T)$ and a binary mask of same length $\boldsymbol{m} = (m_1, \cdots, m_T)$. The generator $G_{\theta}$ and $D_{\phi}$ are \begin{align} G_{\theta}(x_{t}) = P(\hat{x_{t}} | \hat{x}_1, \cdots \hat{x}_{t-1}, \boldsymbol{m(x)}) \end{align} \begin{align} D_{\phi}(\tilde{x}_{t}|\tilde{x}_{0:T}) = P(\tilde{x}_{t} = x^{real}_{t} | \tilde{x}_{0:T}, \boldsymbol{m}(\boldsymbol{x}))\textrm{ ,} \end{align} The reward is defined as the logatithm of the prediction of discriminator, which is \begin{align} r_{t} = \textrm{log}D_{\phi}(\tilde{x}_{t}|\tilde{x}_{0:T})\textrm{ ,} \end{align} The training strategy is similar to previous methods. They first pretrain MaskGAN by MLE then apply REINFORCE with baseline to train the generator. The training of discriminator is the same used in conventional GAN.
Fig 22 shows the human study result of MaskGAN on IMDB review and PTB dataset. For each row, they ask turkers to which model do they prefer or neither do they prefer in terms of Grammaticality, Topicality and Overall. They sample 100 sentece for each model and ask 3 turkers to give their preference. We can see MaskGAN is always preferred by human in all metric.

Evaluation
Despite many automatic metrics are proposed to increase the correlation with human judgment, recent studies~\cite{} point out that existing metrics are poorly correlated with human judgement and biased. Chaganty et al. points out the cost to debias these automatic metrics is about conducting the full human evaluation~\cite{}.
So, back to our question: “How do we properly evaluate the quality of text generation model ?” To my best knowledge, we don’t know.
The evaluation of natural language generation in different setting (e.g., dialog response generation, image to caption, summarization…etc) remain an open research problem. Each has their challenges to be overcome. For text generation model discussed in this post, a specific aspect is whether the model suffer from mode-collpase (lack diversity) in addition to the text quality. A naive approach to measure the diversity is to count unique n-gram. However, such evaluation might suffer an issue that the generatd text only diverse in local but not in global as discussed in MaskGAN paper. The diversity issue has only be discussed in MaskGAN and a recent survey. In addition, there is no existing metrics in text geneation analogous to Inception-Score~\cite{} or Fréchet Inception Distance~\cite{} in conventional GAN that can reflect the diversity and quality of geneated images, which might suggest a direction to explore.
It might sound disappointed that we have barely no idea about what metrics to use to accurately evaluate the text generation model. Current approach normally resort to combination of human judgment and automatic metrics, the former even plays more important role. However, it would be easier to talk about how NOT to evaluate text generation models:
Do not claim any model is superior to others by automatic metric only. There are many aspects of language cannot be reflected by them.
Final Word
Phew! We made it to the end. Although it might take some time to digest, I hope this overview can give you a bird-eye view of recent developments of text generation models.
In summary, generating natural language is a holy grail of text generation research. Current approaches have not yet fully captured the nuances, details and semantic of natural language, which compounds when we generate longer text. A better metric is also necessary for evaluating the generated text and human study is. This post only summarized three lines of text generation research. By the way, there are other interesing methods not belong to the category defined in this post. If you have not get overwhelmed, these two papers I found really interesting. You can check them here and here
Finally, since I am not a senior researcher in this field, I might make mistakes so any comment or suggestion are welcome :)